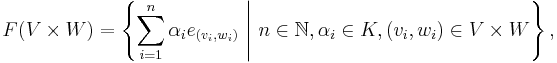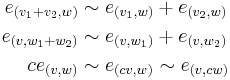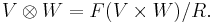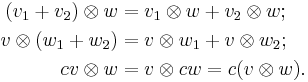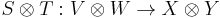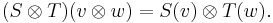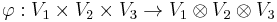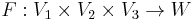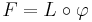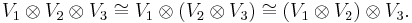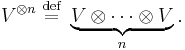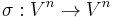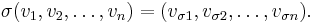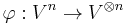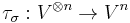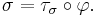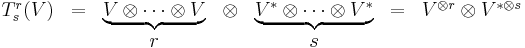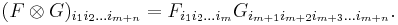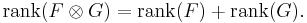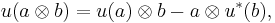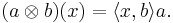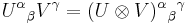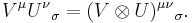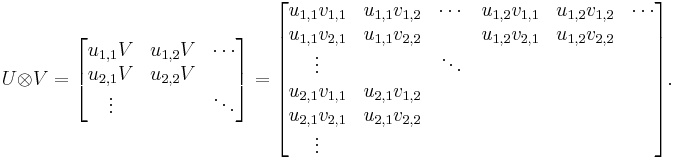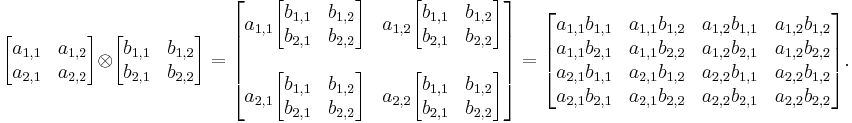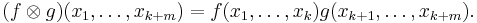Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general bilinear operation. In some contexts, this product is also referred to as outer product. The term "tensor product" is also used in relation to monoidal categories.
Contents |
Tensor product of vector spaces
The tensor product V ⊗ W of two vector spaces V and W over a field K can be defined by the method of generators and relations.
To construct V ⊗ W, one begins with the set of ordered pairs in the Cartesian product V × W. For the purposes of this construction, regard this Cartesian product as a set rather than a vector space. The free vector space F on V × W is defined by taking the vector space in which the elements of V × W are a basis. In set-builder notation,
where we have used the symbol e(v,w) to emphasize that these are taken to be linearly independent by definition for distinct (v, w) ∈ V × W.
The tensor product arises by defining the following four equivalence relations in F(V × W):
where v1, v2, and w1, w2 are vectors from V and W (respectively), and c is from the underlying field K. Denoting by R the space generated by these four equivalence relations, the tensor product of the two vector spaces V and W is then the quotient space
It is also called the tensor product space of V and W and is a vector space (which can be verified by directly checking the vector space axioms). The tensor product of two elements v and w is the equivalence class (e(v,w) + R) of e(v,w) in V ⊗ W, denoted v ⊗ w. This notation can somewhat obscure the fact that tensors are always cosets: manipulations performed via the representatives (v,w) must always be checked that they do not depend on the particular choice of representative.
The space R is mapped to zero in V ⊗ W, so that the above three equivalence relations become equalities in the tensor product space:
Given bases {vi} and {wi} for V and W respectively, the tensors {vi ⊗ wj} form a basis for V ⊗ W (generally ordered so that vi ⊗ wj+1 comes before vi+1 ⊗ wj). The dimension of the tensor product therefore is the product of dimensions of the original spaces; for instance Rm ⊗ Rn will have dimension mn.
Elements of V ⊗ W are sometimes referred to as tensors, although this term refers to many other related concepts as well.[1] An element of V ⊗ W of the form v ⊗ w is called a pure or simple tensor. In general, an element of the tensor product space is not a pure tensor, but rather a finite linear combination of pure tensors. That is to say, if v1 and v2 are linearly independent, and w1 and w2 are also linearly independent, then v1 ⊗ w1 + v2 ⊗ w2 cannot be written as a pure tensor. The number of simple tensors required to express an element of a tensor product is called the tensor rank, (not to be confused with tensor order, which is the number of spaces one has taken the product of, in this case 2; in notation, the number of indices) and for linear operators or matrices, thought of as (1,1) tensors (elements of the space V ⊗ V*), it agrees with matrix rank.
Characterization by a universal property
The tensor product of V and W can be defined (up to isomorphism) by any pair (L, φ), with L a vector space on K and 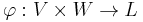 a bilinear map such that
a bilinear map such that
- for any K-vector space Z and any bilinear map
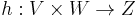 , there exists a unique linear map
, there exists a unique linear map 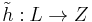 verifying
verifying 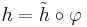
In this sense, φ is the most general bilinear map that can be built from VxW.
It is easy to check that 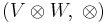 satisfies this universal property.
satisfies this universal property.
As a functor
The tensor product also operates on linear maps between vector spaces. Specifically, given two linear maps S : V → X and T : W → Y between vector spaces, the tensor product of the two linear maps S and T is a linear map
defined by
In this way, the tensor product becomes a bifunctor from the category of vector spaces to itself, covariant in both arguments.[2]
The Kronecker product of two matrices is the matrix of the tensor product of the two corresponding linear maps under a standard choice of bases of the tensor products (see the article on Kronecker products).
More than two vector spaces
The construction and the universal property of the tensor product can be extended to allow for more than two vector spaces. For example, suppose that V1, V2, and V3 are three vector spaces. The tensor product V1 ⊗ V2 ⊗ V3 is defined along with a trilinear mapping from the direct product
so that, any trilinear map F from the direct product to a vector space W
factors uniquely as
where L is a linear map. The tensor product is uniquely characterized by this property, up to a unique isomorphism.
This construction is related to repeated tensor products of two spaces. For example, if V1, V2, and V3 are three vector spaces, then there are (natural) isomorphisms
More generally, the tensor product of an arbitrary indexed family Vi, i ∈ I, is defined to be universal with respect to multilinear mappings of the direct product 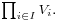
Tensor powers and braiding
Let n be a non-negative integer. The nth tensor power of the vector space V is the n-fold tensor product of V with itself. That is
A permutation σ of the set {1, 2, ..., n} determines a mapping of the nth Cartesian power of V
defined by
Let
be the natural multilinear embedding of the Cartesian power of V into the tensor power of V. Then, by the universal property, there is a unique morphism
such that
The morphism τσ is called the braiding map associated to the permutation σ.
Tensor product of two tensors
A tensor on V is an element of a vector space of the form
for non-negative integers r and s. There is a general formula for the components of a (tensor) product of two (or more) tensors. For example, if F and G are two covariant tensors of rank m and n (respectively) (i.e. F ∈ Tm0, and G ∈ Tn0), then the components of their tensor product are given by
In this example, it is assumed that there is a chosen basis B of the vector space V, and the basis on any tensor space Tsr is tacitly assumed to be the standard one (this basis is described in the article on Kronecker products). Thus, the components of the tensor product of two tensors are the ordinary product of the components of each tensor.
Note that in the tensor product, the factor F consumes the first rank(F) indices, and the factor G consumes the next rank(G) indices, so
The tensor 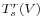 may be naturally viewed as a module for the Lie algebra
may be naturally viewed as a module for the Lie algebra 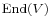 by means of the diagonal action: for simplicity let us assume
by means of the diagonal action: for simplicity let us assume 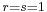 , then, for each
, then, for each 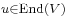 ,
,
where 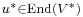 is the transpose of
is the transpose of 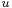 , that is, in terms of the obvious pairing on
, that is, in terms of the obvious pairing on 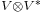 ,
,
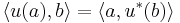 .
.
There is a canonical isomorphism 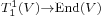 given by
given by
Under this isomorphism, every 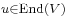 may be first viewed as an endomorphism of
may be first viewed as an endomorphism of 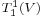 and then viewed as an endomorphism of
and then viewed as an endomorphism of 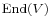 . In fact it is the adjoint representation
. In fact it is the adjoint representation 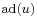 of
of 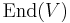 .
.
Example
Let U be a tensor of type (1,1) with components Uαβ, and let V be a tensor of type (1,0) with components Vγ. Then
and
The tensor product inherits all the indices of its factors.
Kronecker product of two matrices
With matrices this operation is usually called the Kronecker product, a term used to make clear that the result has a particular block structure imposed upon it, in which each element of the first matrix is replaced by the second matrix, scaled by that element. For matrices 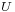 and
and 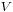 this is:
this is:
For example, the tensor product of two two-dimensional square matrices:
The resultant rank is at most 4, and the resultant dimension 16. Here rank denotes the tensor rank (number of requisite indices), while the matrix rank counts the number of degrees of freedom in the resulting array.
A representative case is the Kronecker product of any two rectangular arrays, considered as matrices. A dyadic product is the special case of the tensor product between two vectors of the same dimension.
Tensor product of multilinear maps
Given multilinear maps 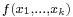 and
and 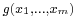 their tensor product is the multilinear function
their tensor product is the multilinear function
Relation with the dual space
In the discussion on the universal property, replacing X by the underlying scalar field of V and W yields that the space 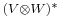 (the dual space of
(the dual space of 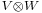 , containing all linear functionals on that space) is naturally identified with the space of all bilinear functionals on
, containing all linear functionals on that space) is naturally identified with the space of all bilinear functionals on 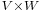 . In other words, every bilinear functional is a functional on the tensor product, and vice versa.
. In other words, every bilinear functional is a functional on the tensor product, and vice versa.
Whenever 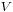 and
and 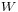 are finite dimensional, there is a natural isomorphism between
are finite dimensional, there is a natural isomorphism between  and
and 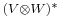 , whereas for vector spaces of arbitrary dimension we only have an inclusion
, whereas for vector spaces of arbitrary dimension we only have an inclusion 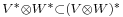 . So, the tensors of the linear functionals are bilinear functionals. This gives us a new way to look at the space of bilinear functionals, as a tensor product itself.
. So, the tensors of the linear functionals are bilinear functionals. This gives us a new way to look at the space of bilinear functionals, as a tensor product itself.
Types of tensors
Linear subspaces of the bilinear operators (or in general, multilinear operators) determine natural quotient spaces of the tensor space, which are frequently useful. See wedge product for the first major example. Another would be the treatment of algebraic forms as symmetric tensors.
Over more general rings
The notation ⊗R refers to a tensor product of modules over a ring R.
Tensor product for computer programmers
Array programming languages
Array programming languages may have this pattern built in. For example, in APL the tensor product is expressed as 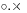 (for example
(for example 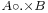 or
or 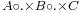 ). In J the tensor product is the dyadic form of */ (for example a */ b or a */ b */ c).
). In J the tensor product is the dyadic form of */ (for example a */ b or a */ b */ c).
Note that J's treatment also allows the representation of some tensor fields, as a and b may be functions instead of constants. This product of two functions is a derived function, and if a and b are differentiable, then a*/b is differentiable.
However, these kinds of notation are not universally present in array languages. Other array languages may require explicit treatment of indices (for example, MATLAB), and/or may not support higher-order functions such as the Jacobian derivative (for example, Fortran/APL).
See also
- Extension of scalars
- Tensor product of R-algebras
- Tensor product of fields
- Tensor product of graphs
- Tensor product of Hilbert spaces
- Tensor product of line bundles
- Tensor product of modules
- Tensor product of quadratic forms
- Topological tensor product
- Dyadic product
- Tensor contraction
Notes
- ^ See tensor or tensor (intrinsic definition).
- ^ Hazewinkel, et. al. (2004), p. 100.
- ^ Analogous formulas also hold for contravariant tensors, as well as tensors of mixed variance. Although in many cases such as when there is an inner product defined, the distinction is irrelevant.
References
- Bourbaki, Nicolas (1989), Elements of mathematics, Algebra I, Springer-Verlag, ISBN 3-540-64243-9.
- Halmos, Paul (1974), Finite dimensional vector spaces, Springer, ISBN 0387900934.
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR1878556
- Mac Lane, S.; Birkhoff, G. (1999), Algebra, AMS Chelsea, ISBN 0-8218-1646-2.
- Hazewinkel, Michiel; Gubareni, Nadezhda Mikhaĭlovna; Gubareni, Nadiya; Kirichenko, Vladimir V. (2004), Algebras, rings and modules, Springer, ISBN 9781402026904.